冒泡
步骤
- 从头开始,每次比较两元素,若大者在前,则交换两元素,直至数组末尾,此时最大元素为数组最后的元素;
- 重复以上步骤,从头开始至上一轮比较的末尾元素;
性质
- 稳定算法;
代码
// 冒泡排序
void bubbleSort(vector<int>& array) {
for (size_t i = 0; i < array.size(); i++) {
// 当前轮是否发生过交换事件标志位,若未发生交换,则表明列表已有序。
bool isExchanged = false;
for (size_t j = 0; j < array.size() - i - 1; j++) {
if (array[j] > array[j + 1]) {
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
isExchanged = true;
}
}
if (!isExchanged){
break;
}
}
}
选择
步骤
- 搜索整个列表,找出最小项,若此项不为第1项,则与第1项交换位置;
- 重复上述步骤,每次搜索未被排序的剩余列表,并将最小元素与已排序段的后一位交换,直至列表所有元素均被排序;
性质
- 不稳定算法;
代码
// 选择排序
void selectSort(vector<int>& array){
for (size_t i = 0; i < array.size(); i++){
size_t minIndex = i;
for (size_t j = i + 1; j < array.size(); j++){
if (array[minIndex] > array[j]){
minIndex = j;
}
}
if (minIndex != i){
swap(array[i], array[minIndex]);
}
}
}
插入
步骤
- 将第一个元素看作有序序列,后续元素当作无需序列,依次将无序序列元素插入有序序列当中;
性质
- 稳定算法;
代码
// 插入排序
void insertionSort(vector<int>& array){
// i 代表无序序列首元素(无序序列前为有序序列)
size_t i = 1;
while (i < array.size()){
size_t j = i - 1;
int itermToInsert = array[i];
while (j >= 0){
if (array[j] >= itermToInsert){
array[j + 1] = array[j];
j--;
}
else{
break;
}
}
array[j + 1] = itermToInsert;
i++;
}
}
希尔
步骤
- 选择一个增量序列,初始增量gap=length/2,后续元素依次为前一元素除2,直至gap=1;
- 每轮以gap为步长,在列表上进行采样,将列表分为gap个小组,在每个小组内进行选择排序;
- 重复第二步,直至gap=1;
性质
- 不稳定算法;
代码
// 希尔排序
void shellSort(vector<int>& array){
int n = array.size();
for (int gap = n / 2; gap >= 1; gap /= 2){
for (int i = gap; i < n; i++){
// 使用插入排序算法,将元素依次插入所在小组的已排序列表中
// 待插入元素
int itermToInsert = array[i];
int j = i - gap;
while (j >= 0 && array[j] >= itermToInsert){
array[j + gap] = array[j];
j -= gap;
}
array[j + gap] = itermToInsert;
}
}
}
归并
步骤
- 将列表从正中间分为两个子列表;
- 按照第一步,递归拆分每个子列表,直至子列表最大长度为1;
- 按照拆分层级,依次按大小合并各子列表,直至全部合并完成。
性质
- 稳定算法;
代码
递归实现
// 归并排序
// 合并两有序序列,两序列分别为array的0到mid部分和mid+1到末尾部分。
void merge(vector<int>& array, vector<int>& copyArray, int left, int right) {
int mid = (left + right) / 2;
int i = left, j = mid + 1, k = 0;
while (i <= mid || j <= right) {
if (i > mid) {
copyArray[k] = array[j];
j++;
}
else if (j > right) {
copyArray[k] = array[i];
i++;
}
else if (array[i] > array[j]) {
copyArray[k] = array[j];
j++;
}
else {
copyArray[k] = array[i];
i++;
}
k++;
}
for (size_t i = left; i <= right; i++) {
array[i] = copyArray[i - left];
}
}
void mergeSortHelp(vector<int>& array, vector<int>& copyArray, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
mergeSortHelp(array, copyArray, left, mid);
mergeSortHelp(array, copyArray, mid + 1, right);
merge(array, copyArray, left, right);
}
}
// 归并排序 递归实现
void mergeSort(vector<int>& array) {
vector<int> copyArray(array);
mergeSortHelp(array, copyArray, 0, array.size() - 1);
}
迭代实现
// 归并排序 迭代实现
void mergeSortIteration(vector<int>& array) {
vector<int> copyArray(array);
int left = 0, right = array.size() - 1;
stack<vector<int>> boundaries;
while (left < right || !boundaries.empty()) {
if (left < right) {
boundaries.push({ left, right });
right = (left + right) / 2;
}
else {
vector<int> boundary = boundaries.top();
boundaries.pop();
left = boundary[0];
right = boundary[1];
merge(array, copyArray, left, right);
if (boundaries.empty()) {
break;
}
boundary = boundaries.top();
left = right + 1;
right = boundary[1];
}
}
}
快速
步骤
- 从列表中选出一个元素,作为“基准”pivot,基准一般随机选择,或采用最左端、最右端和中间位置3元素的中值;
- 将小于基准的元素排在基准前面,大于基准的元素排在基准后面,此时基准元素所在位置即为其最终排序完成时的位置;
- 以基准元素为界,将列表分为两个子列表;
- 递归地对子列表重复上述操作。
性质
- 不稳定算法;
- 当数据量很小(N<=20)时,快速排序效果不如插入排序,因为快速排序不稳定且有递归开销;
代码
递归版:
递归版:
// 快速排序(递归)
// 选则最左端、最右端和中间位置3元素的中值作为基准值,并将3元素排序,返回基准值
int medianPovit(vector<int>& array, int left, int mid, int right){
if (array[left] > array[mid]){
swap(array[mid], array[left]);
}
if (array[left] > array[right]){
swap(array[left], array[right]);
}
if (array[mid] > array[right]){
swap(array[mid], array[right]);
}
return array[mid];
}
// 分区,返回基准索引
int partition(vector<int>& array, int left, int right) {
// 中间位置索引
int mid = (left + right) / 2;
// 基准值(此时基准值对应索引为mid)
int povit = medianPovit(array, left, mid, right);
// 将基准值与倒数第二个元素交换
array[mid] = array[right - 1];
array[right - 1] = povit;
int i = left, j = right - 1;
while (i < j) {
if (array[i] < povit) {
i++;
}
else if (array[j] >= povit) {
j--;
}
else {
swap(array[i], array[j]);
}
}
// 交换基准值和i位置元素
swap(array[i], array[right - 1]);
return i;
}
void quickSortHelp(vector<int>& array, int left, int right) {
if (left < right) {
int pivotLoction = partition(array, left, right);
quickSortHelp(array, left, pivotLoction - 1);
quickSortHelp(array, pivotLoction + 1, right);
}
}
// 快速排序
void quickSort(vector<int>& array) {
quickSortHelp(array, 0, array.size() - 1);
}
迭代版:
// 快速排序 非递归(迭代版)
void quickSortIteration(vector<int>& array) {
stack<vector<int>> boundaries;
int left = 0, right = array.size() - 1;
while (left < right || !boundaries.empty()) {
if (left >= right) {
vector<int> boundary = boundaries.top();
boundaries.pop();
left = boundary[0];
right = boundary[1];
}
int pivotLoction = partition(array, left, right);
if (pivotLoction + 1 < right) {
boundaries.push({ pivotLoction + 1, right });
}
right = pivotLoction - 1;
}
}
堆排序
步骤
-
将数字转化为一个堆;
堆是具有以下两属性的二叉树:
(1)每个节点的值大于等于其子节点的值;
(2)树完全平衡,即最底层叶子节点都位于左侧(完全),且左右子树高度相差不超过1(平衡);
因为,堆是完全平衡树,因此可以用数组直接表示:
堆也被称为优先队列,具有先进先出的特性,在堆底插入元素,在堆顶取出元素。
-
取出堆顶元素(最大元素),作为有序数数组末尾元素,并对二叉树进行调整使其满足堆的特性;
-
重复上一步骤,依次取出堆顶元素,并插入到有序数组中,上一插入元素之前的位置,直到堆空为止;
性质
- 不稳定算法;
代码
// 堆排序
// 调整堆,根元素沿树向下移动,直至其合适位置,first和last分别为堆顶和堆底在数组array中的索引
void moveDown(vector<int>& array, int first, int last){
// first的左子节点索引
int curIndex = first * 2 + 1;
while (curIndex <= last){
// 若first有2子节点,令curIndex为其值最大子节点索引
if (curIndex < last && array[curIndex] < array[curIndex + 1]){
curIndex++;
}
// 若根节点值小于子节点值,则交换
if (array[first] < array[curIndex]){
swap(array[first], array[curIndex]);
first = curIndex;
curIndex = first * 2 + 1;
}
else{
break;
}
}
}
// 用数组实现堆
void buildHeap(vector<int>& array){
// 最后一个非叶节点的节点索引
int i = array.size() / 2 - 1;
while (i >= 0){
moveDown(array, i, array.size() - 1);
i--;
}
}
// 堆排序
void heapSort(vector<int>& array){
// 生成堆
buildHeap(array);
// 堆顶、底索引
int first = 0, last = array.size() - 1;
while (first <= last){
swap(array[first], array[last]);
last--;
moveDown(array, first, last);
}
}
计数排序
步骤
- 遍历待排序数组A,找出其最小值min和最大值max;
- 创建一个长度为max-min+1的数组B,其所有元素初始化为0,数组首位对应数组A的min元素,索引为i位置对应A中值为min+i的元素;
- 遍历数组A,在B中对应位置记录A中各元素出现的次数;
- 遍历数组B,按照之前记录的出现次数,输出几次对应元素;
性质
- 稳定排序算法;
- 外部排序;
代码
// 计数排序
void countSort(vector<int>& array){
if (array.empty()){
return;
}
//找出最大最小值
int min = array.front(),max = array.front();
for (int i = 1; i < array.size(); i++){
if (min > array[i]){
min = array[i];
}
else if (max < array[i]){
max = array[i];
}
}
// 记录各元素出现次数
vector<int> counts(max - min + 1);
for (int i = 0; i < array.size(); i++){
counts[array[i] - min]++;
}
// 根据记录的次数输出对应元素
int index = 0;
for (int j = 0; j < counts.size(); j++){
int n = counts[j];
while (n--){
array[index] = j + min;
index++;
}
}
}
桶排序
步骤
- 设置固定数量的空桶;
- 找出待排序数组的最大值和最小值;
- 根据最大最小值平均划分各桶对应的范围,并将待排序数组放入对应桶中;
- 为每个不为空的桶中数据进行排序(例如,插入排序);
- 拼接不为空的桶中数据,得到排序后的结果。
特性
- 稳定算法;
- 常见排序算法中最快的一种;
- 适用于小范围(最大值和最小值差值较小),独立均匀分布的数据;
- 可以计算大批量数据,符合线性期望时间;
- 外部排序方式,需额外耗费n个空间;
代码
// 桶排序
void bucketSort (vector<int>& array, int bucketCount){
if (array.empty()){
return;
}
// 找出最大最小值
int max = array.front(), min = array.front();
for (int i = 1; i < array.size(); i++){
if (min > array[i]){
min = array[i];
}
else if (max < array[i]){
max = array[i];
}
}
// 将待排序的各元素分入对应桶中
vector<vector<int>> buckets(bucketCount);
int bucketSize = ceil((double)(max - min + 1) / bucketCount);
for (int i = 0; i < array.size(); i++){
int bucketIndex = (array[i] - min) / bucketSize;
buckets[bucketIndex].push_back(array[i]);
}
// 对各桶中元素进行选择排序
int index = 0;
for (vector<int> bucket : buckets){
if (!bucket.empty()){
// 使用选择排序算法对桶内元素进行排序
selectSort(bucket);
for (int value : bucket){
array[index] = value;
index++;
}
}
}
}
// 桶排序
void bucketSort (vector<int>& array){
bucketSort (array, array.size() / 2);
}
基数排序
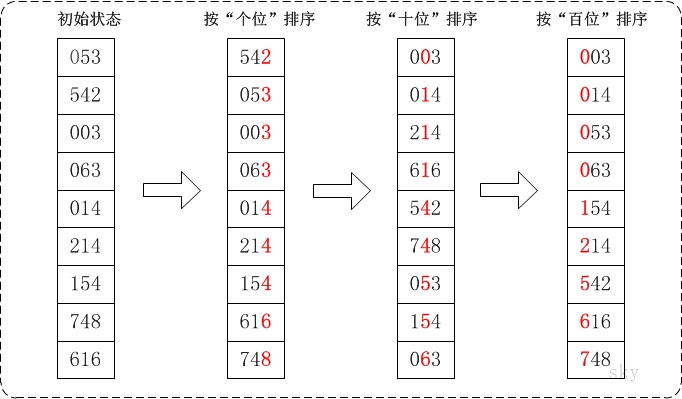
步骤
-
将各待比较元素数值统一数位长度,即对数位短者在前补零;
-
根据个位数值大小,对数组进行排序;
-
重复上一步骤,依次根据更高位数值进行排序,直至到达最高位;
特性
- 稳定算法;
- 适用于正整数数据(若包含负数,那么需要额外分开处理);
- 对于实数,需指定精度,才可使用此算法。
代码
// 基数排序 (只适用于正数,此处不适用)
void radixSort(vector<int>& array){
// 当前位数
int curdigit = 10;
// 当前位是否已超过最高为
bool isOverHighest = false;
while (!isOverHighest){
isOverHighest = true;
// 利用分桶的思想来实现按各位进行排序
vector<vector<int>> buckets(10);
for (int curVal : array){
int bucketIndex = curVal % curdigit - curVal % (curdigit / 10);
buckets[bucketIndex].push_back(curVal);
if (isOverHighest && curVal / curdigit){
isOverHighest = false;
}
}
// 按照桶的顺序,将各桶内元素拼接起来
int index = 0;
for (vector<int> bucket : buckets){
for (int value : bucket){
array[index] = value;
index++;
}
}
curdigit *= 10;
}
}